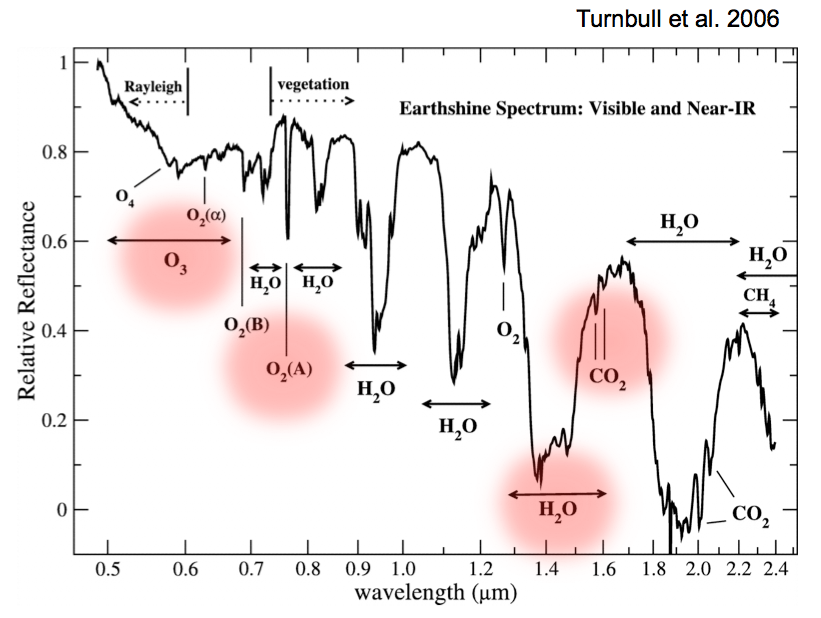
行星大气¶
除了行星的轨道的信息,我们同样想要知道行星本身的性质,比如密度,成分,甚至大气。
通过平均质量和密度关系,我们可以判断行星的可能成分。
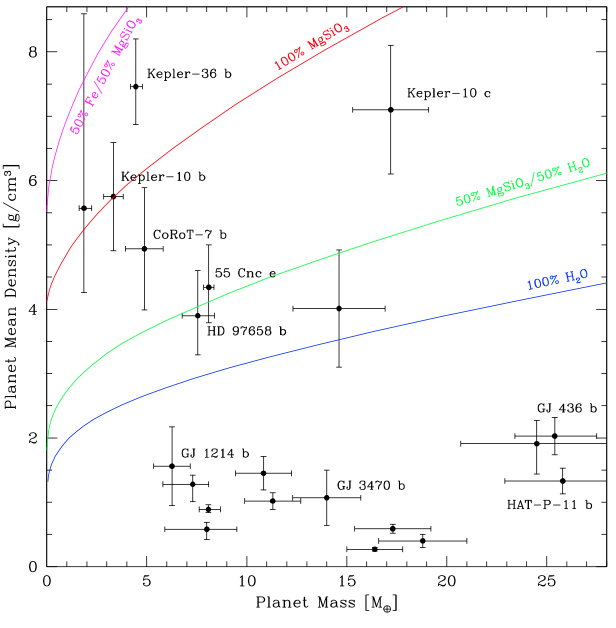
图片:C. Lovis April 2014. 可见行星的质量和平均密度差别很大。红线是指的完全由岩石组成的行星,蓝线是完全由水组成的行星。
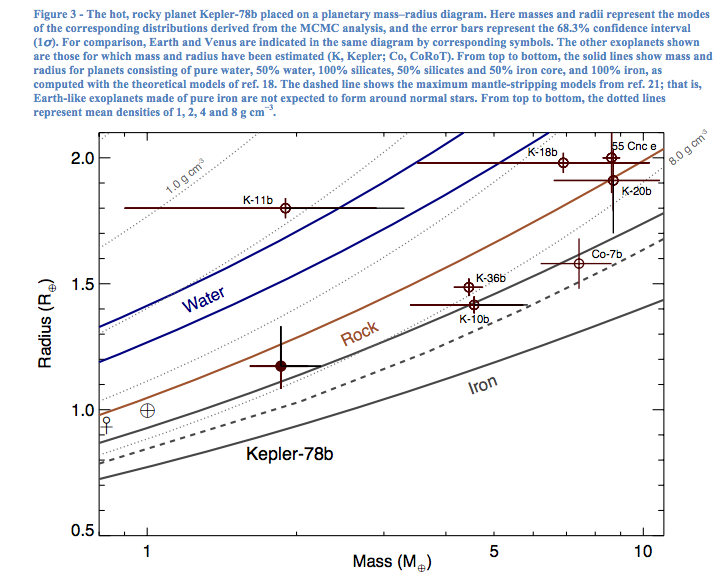
图片来源:arXiv:1310.7987 . 半径-质量图。
我们发现的行星中,有很多质量密度关系很奇怪的行星,目前数据还不足以理解。为了获取更多的信息,一个比较重要的方法是获得行星的光谱,从而获得行星的化学成分的信息。
基础知识¶
理解光谱¶
几个有用的概念
可以从 wikipedia 来获取相关词条,来了解更多的相关知识。
- 黑体辐射
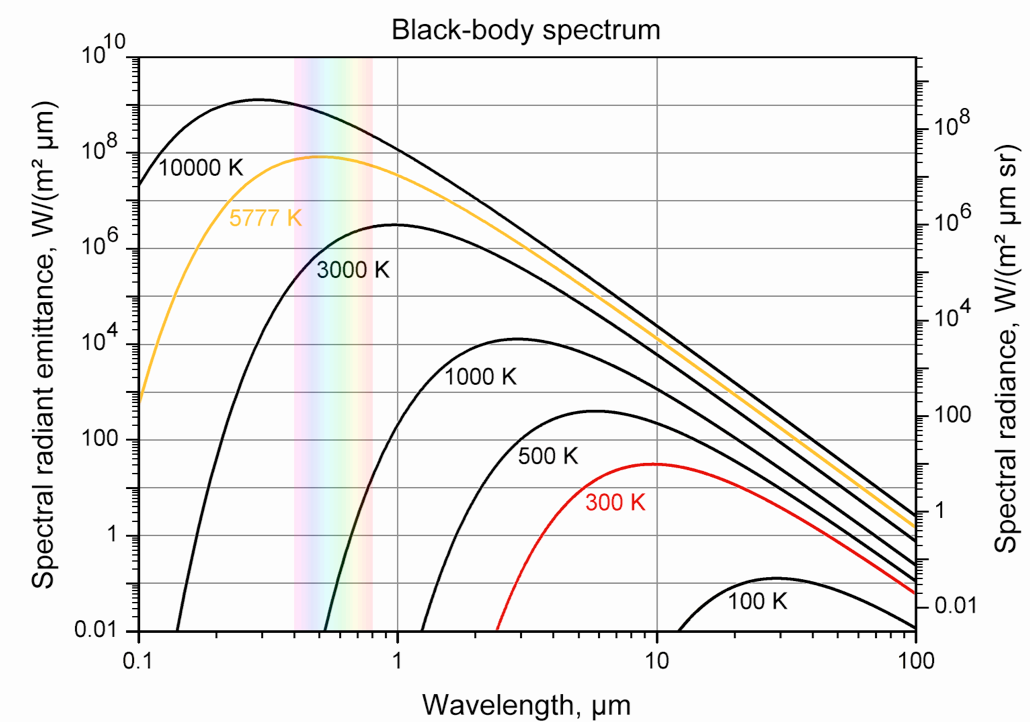
黑体谱是理想的情况下,完全平衡的情况下的光谱。可见光只占了黑体谱的很小的一部分。
- 热平衡
实际上天体物理中常用的是局域的热平衡(Local Thermal Equilibrium, LTE)。
- 辐射转移
- 光深度
下图是几种可能的光谱,光谱确实可能为我们提供很多的信息。
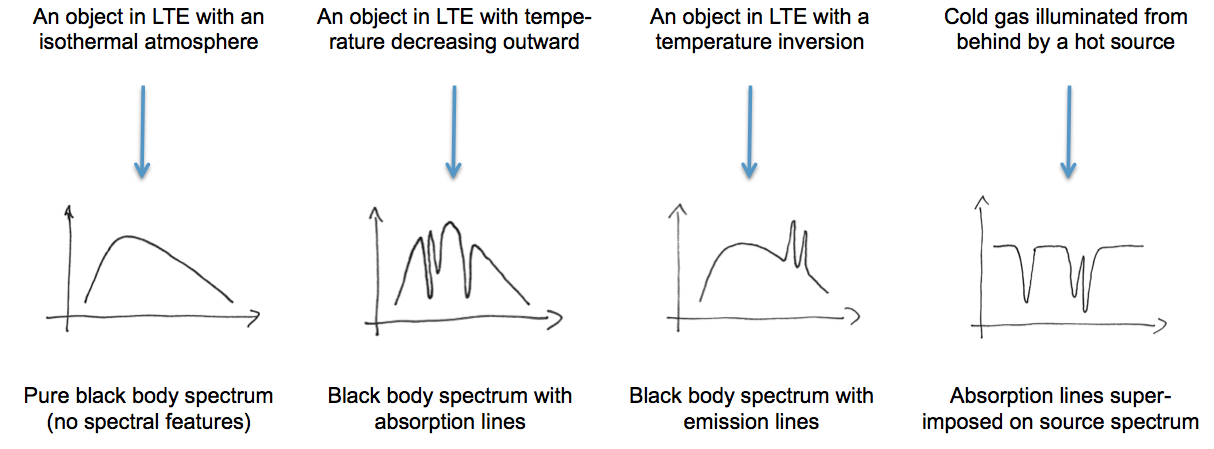
第一种是黑体谱,没有吸收,没有部分衰减;第二种是光源有温度差,不同温度的分层,越往外温度越低,会对不同波长的电磁波有不同的吸收和发射;第三种是越往外温度越高的温度差异;第四种是一个气体被背后的光源照亮,然后产生的吸收谱。
化学成分¶
系外行星上有哪些化学成分呢?
先来看看我们太阳系的情况
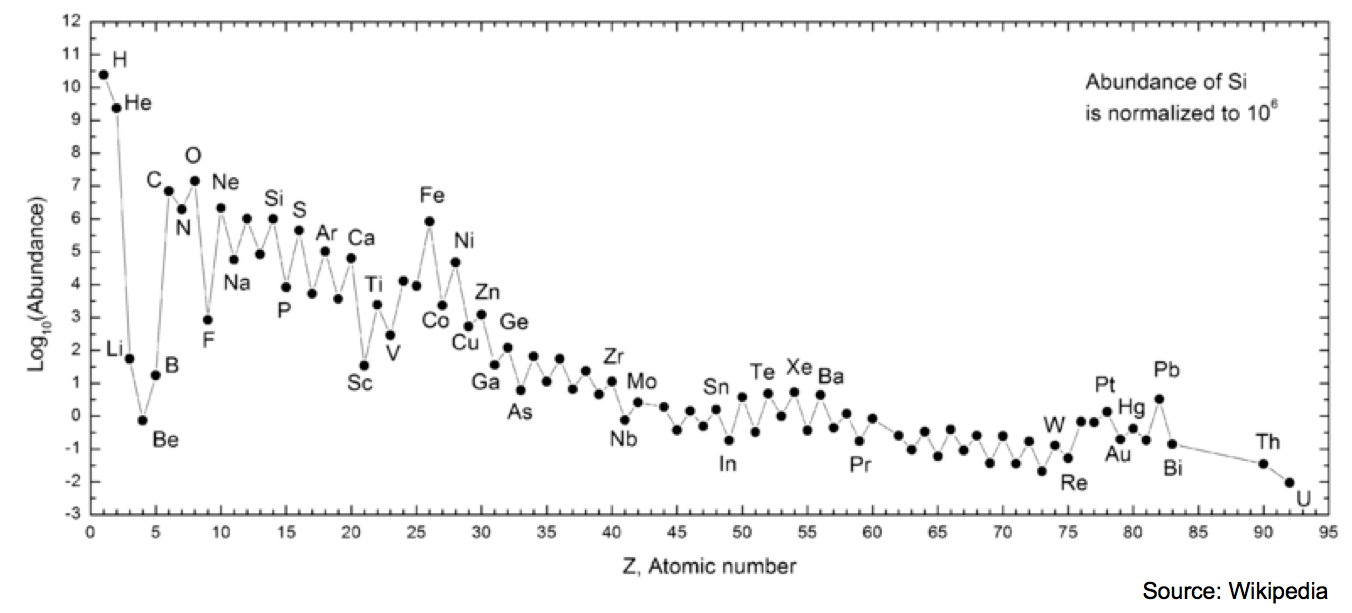
氢和氦是最多的,其次是氧、碳和氮。原子数越多,基本上含量迅速减少。
有了元素的分布,我们可以定性的估计哪些化学成分会比较多。
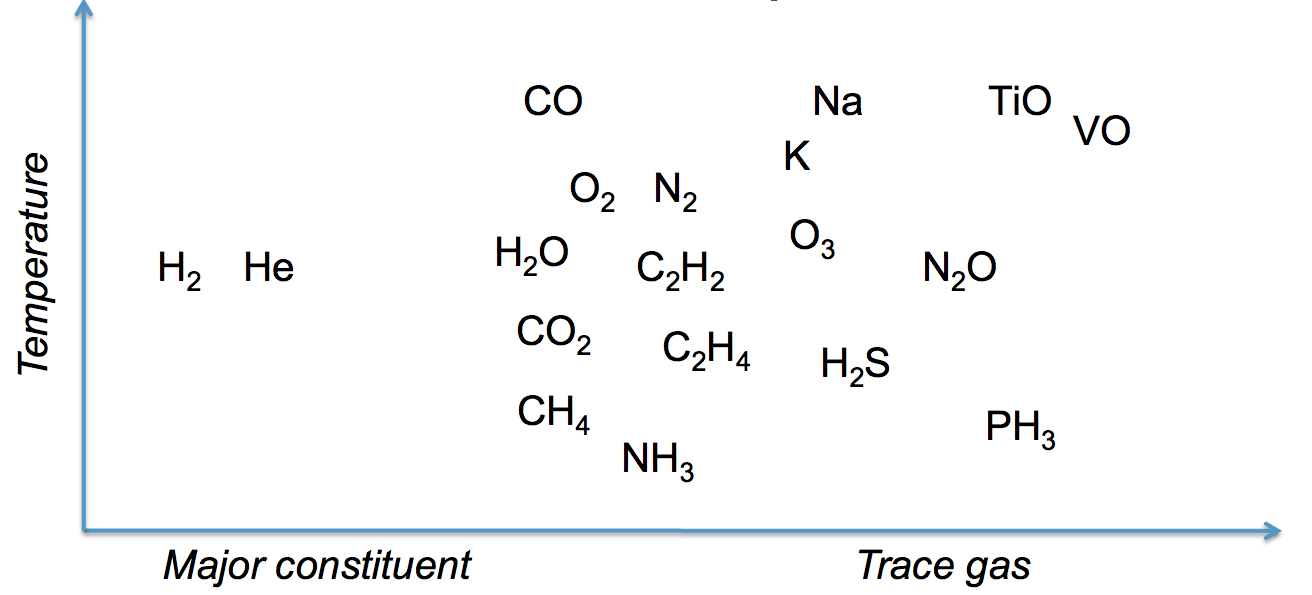
氢气,氦气,各类氧化物,氮化物。根据温度的不同,可能的存在状态也不同。
那么如何探测这些化学成分呢?一种可行的方法是使用光谱。我们可以计算辐射转移方程来获得最终的可能的光谱。一些可能的化学成分的特征可以从下面的几点来获得。
- 分子原子的电子跃迁会产生不同的谱线;
- 分子的转动-振动谱线;
- 散射,包括瑞利散射(散射粒子远小于光波长)和米散射(散射粒子大于光波长)。
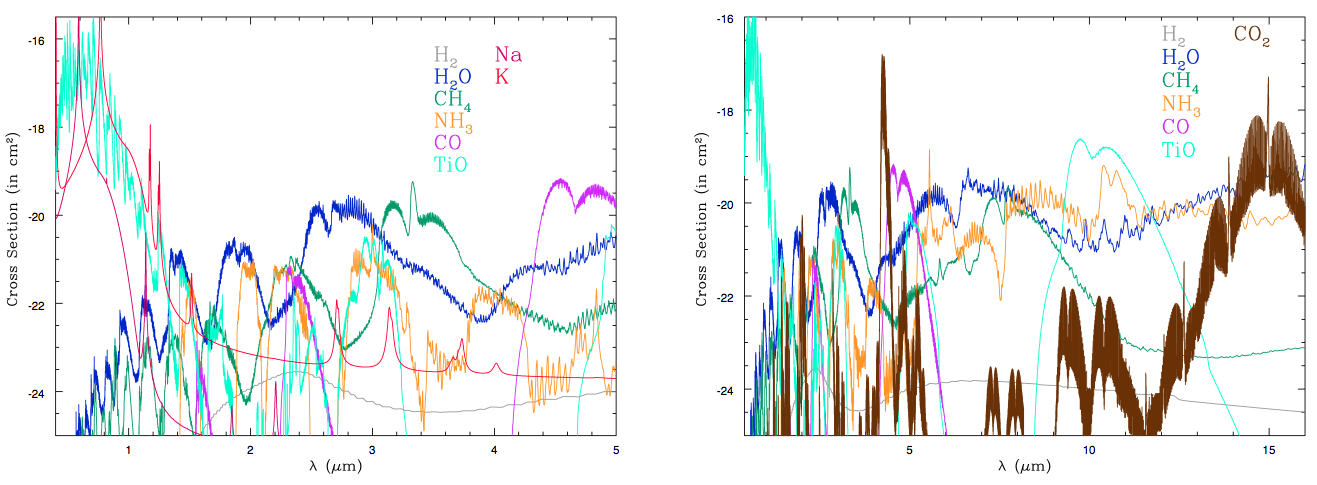
对于不同的波长,不同的化学分子有不同的散射界面。散射界面越小,就显得越透明。来源:Burrows 2014
图中有一个有趣的例子是二氧化碳。二氧化碳的散射界面在波长比较长的时候变得很大,可以将这些波长“囚禁”起来,而这些波长正好是产生热效应的波长,所以二氧化碳是一种温室气体。
压强-温度关系¶
大气压强——热力学
我们可以导出大气压强和高度的关系(近似)
方程左边是压力差/面积,方向向上,右边是单位体积的重力作用,方向向下,所以有个负号。通过量纲检查发现这个方程量纲正确。
从物理本科的热力学课程,对于理想气体,我们可以知道状态方程是
这样把第二个方程代入第一个方程,可以导出压强随着高度变化的解,
其中 \(H=\frac{kT}{\mu g}\) .
大气中的能量的传输有两种主要的方式,辐射和对流,这两种方式都可以跟温度差有关。
区分恒星光谱和行星光谱¶
如果要区分两者光谱,理想的情况是我们能够直接有足够的角分辨率,从而能够从仪器中直接将行星和恒星分开。然而这是非常困难的。除了角分辨率的问题,行星相比于恒星实在太暗了,要比恒星暗 \(10^{-3}\) 到 \(10^{-10}\) 倍。
几个数字
假定我们从 10pc 远的地方看太阳系,想要分辨出地球和太阳,那么我们需要最小 0.1 弧秒的分辨率。然而,光学望远镜有一个光学上的衍射极限,直径 1.3m 的望远镜,衍射极限就是 0.1 弧秒,角分辨率不能比这个更加小。
然而技术的进步,我们现在已经能够直接看到一些行星了。例如 HR 8799

这是些年轻的行星,行星本身的温度比较高,而且距离恒星比较远,所以探测起来要容易的多。然而,更加吸引我们的是那些像地球一样的行星,所以我们暂时还需要寻求另外的方法。
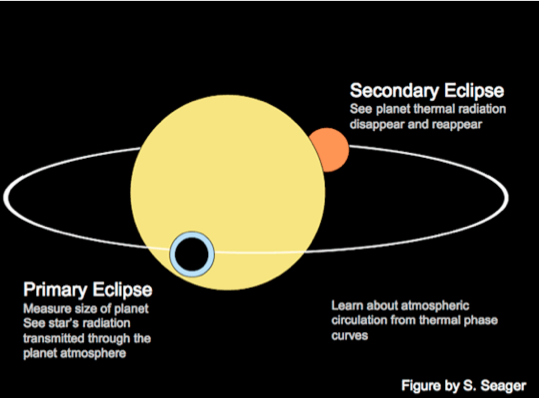
一个很神奇的方法是使用凌日。当行星位于我们和恒星之间的时候,我们看到的光谱是包括行星的,但是当行星移动到恒星的背面,我们观测到的光谱就没有行星的成分了。通过对照这两类光谱,我们可以获得一些行星光谱的信息。
透射光谱¶
前面我们看到,对于不同的波长,大气的透明度不同,所以当我们观测不同的波长的时候,我们会看到不同大小的行星。对于某些相对大气不透明的波长,因为行星大气底层密度大的区域阻止了光的通过,所以会看到一个更大的行星。当我们观测另外一些特别透明的波长的时候,我们会看到更小的行星。
透射
行星的大气层越厚对光的吸收就越好,但是对于不同的波长的吸收不同。有的波长吸收多,可以被相对比较高层的大气遮挡,这时候我们通过这个波段观察行星就会看到一个更大的行星。然而有的波长不容易被吸收,这时候我们观测到的是一个更小的行星,因为高层的大气不能遮挡这个波段。
我们可以计算大气在什么样的高度上就变得透明了,当然这个透明度跟散射界面有关。
也就是说,散射界面越大,这个高度就越大。而这里面 \(H=\frac{kT}{\mu g}\) 是一个跟行星大气的特征有关的量。这样我们结合不同波长的观测的结果,就可以计算行星大气。另外,我们还可以根据对不同波长的透明度推断行星大气的化学成分。
实例
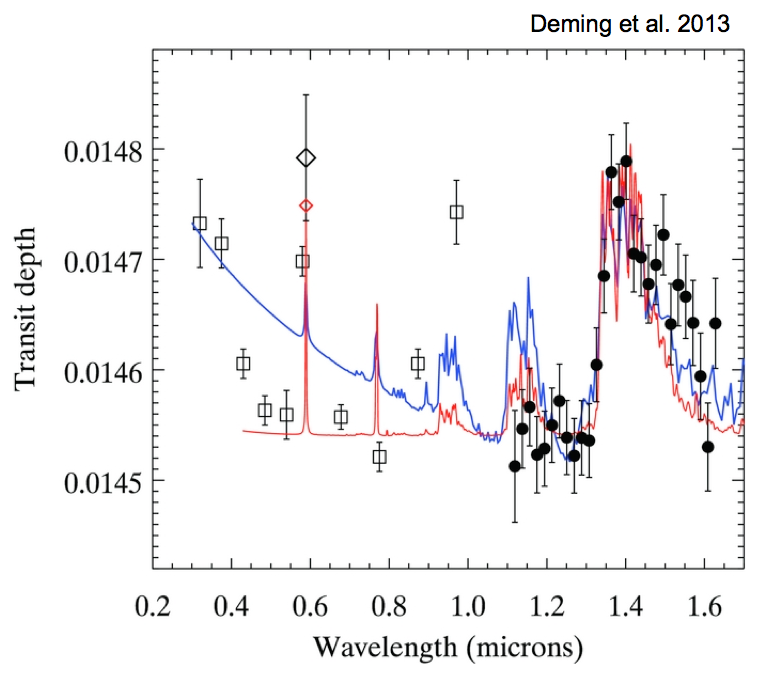
HD 209458b, 右侧的巨大的峰值显示了水蒸气的透射波长。
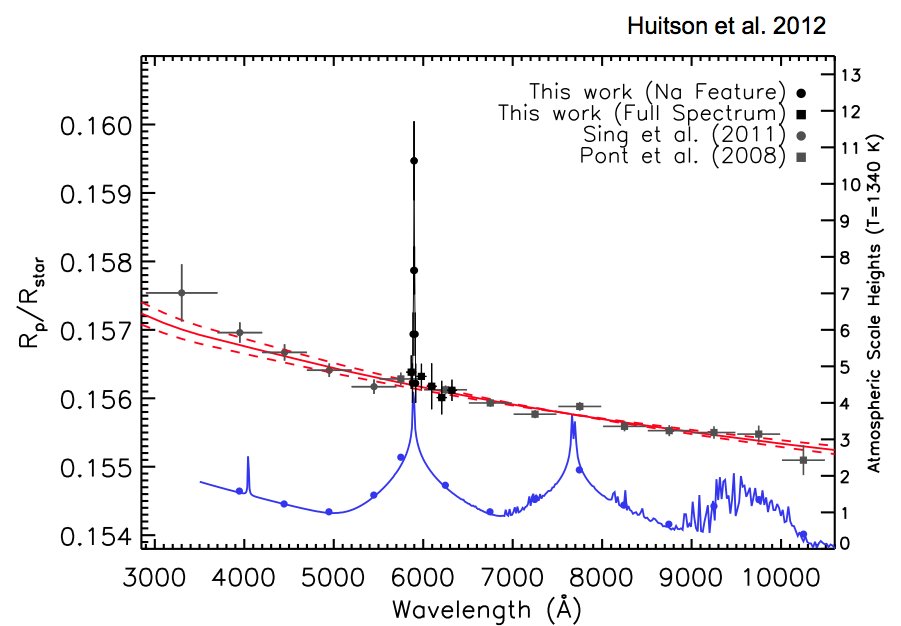
HD 189733b,红线是观测结果,逐渐降低的半径显示了很可能有雾气或者云层导致瑞利散射。
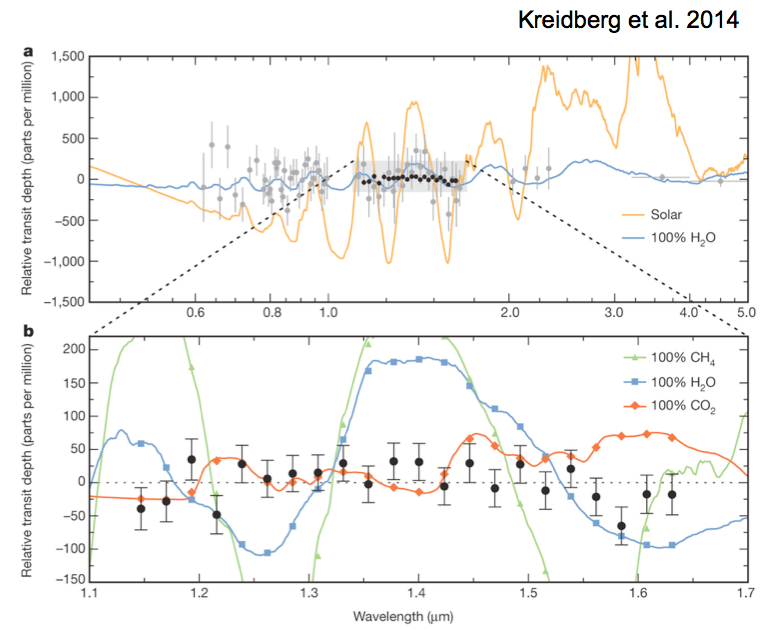
GJ 1214b,几乎水平的结果暗示这颗行星有云层或者雾气。
热发射谱¶
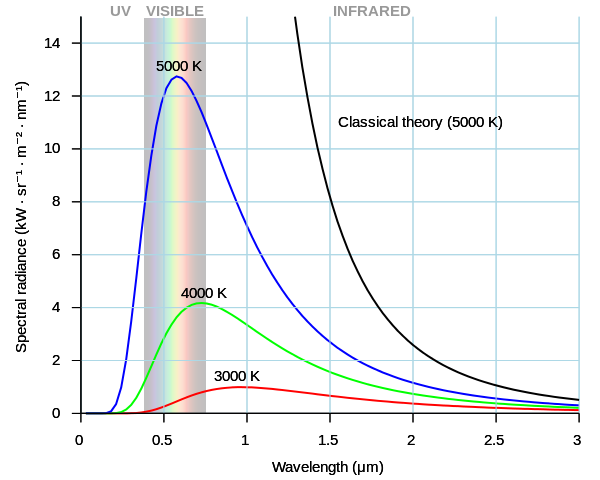
黑体辐射
如果行星吸收的所有的能量跟他释放的能量相同,那么这个行星处在热平衡,这时候(吸收或者放出的能量所对应)的温度叫做平衡温度 \(T_{eq}\) ;如果我们假定行星是黑体,他放出的总的辐射的能量,所对应的黑体温度,就做有效温度 \(T_{eff}\) 。通过计算,我们可以得出
其中 \(A_B\) 是 bond albedo,即没有被吸收的能量占总的入射能量的比值。
我们可以定义热发射流量比,即恒星的热发射的流量与恒星的比值,
可以发现右侧是一些跟轨道半长轴 a,恒星行星半径 \(R_p\) ,恒星半径 \(R_s\) ,\(A_B\) 有关的量,而左边是观测值,这样我们通过对不同波长的对比,可以得到很多行星大气的信息。
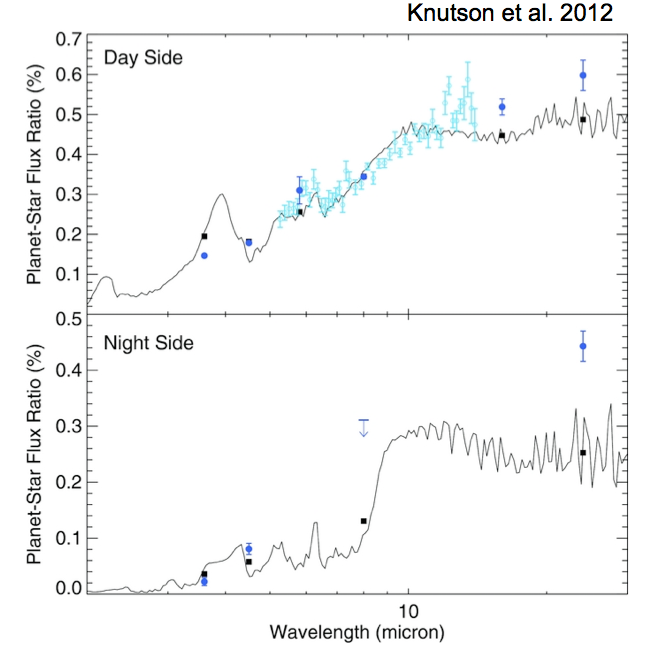
HD 189733b,一颗被潮汐锁定的行星,下面一张图是夜晚部分的曲线,显然要比白天部分的要冷。